Распределенная нагрузка q = 40000 Н/м.пог.
Марка бетона M 200 (класс бетона B15) – по таблице 8.5.
Требуется произвести расчет деформаций балки.
Жесткость В изгибаемых свободноопертых элементов прямоугольного сечения определяется по формуле:
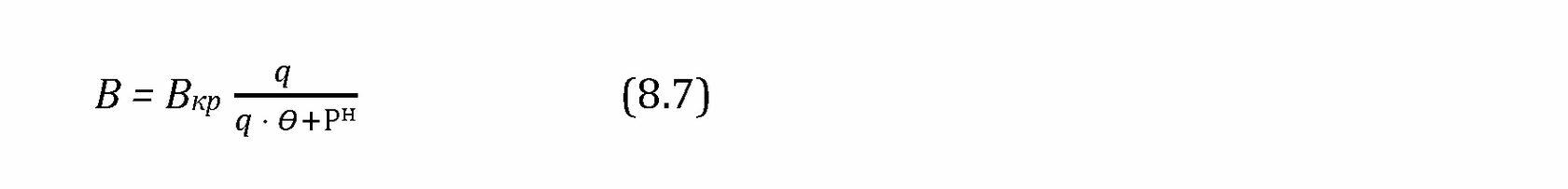
θ - коэффициент, учитывающий уменьшение жесткости при длительном действии нагрузки (для элементов прямоугольного сечения принимается равным 2),
Рн – собственный вес балки.
Рн = h · b · γбетона ; (γбетона = 24000н/ м³) Вкр – критическая жесткость, которая рассчитывается по формуле:

где Еа – модуль упругости арматуры,
Fa – площадь принимаемой арматуры,

- средняя высота сжатой зоны,
h0 – рабочая высота сечения (рисунок 8.2),
а – защитный слой арматуры;

Еб – модуль упругости бетона.
По предыдущему расчету была принята арматура класса А-III, ø25 мм (Fa= 9,82 см² при двух стержнях).
1. Модуль упругости определяем для тяжелого бетона по табл. 8.7
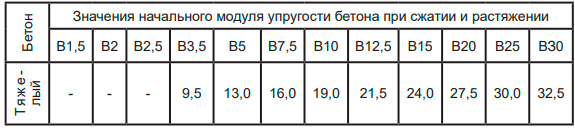
Таблица 8.7 – Значения модуля упругости бетона (Таблица 6.11 СП13330.3012)
Модуль упругости арматуры Es принимают по СП63.13330.2012 п. 6.2.12. Es = 2·105 МПа для арматуры класса А и В.
Рассчитаем коэффициент а (коэффициент армирования μ для ригеля примем равным 0,05) по формуле (8.9):

2. Рассчитаем среднюю высоту сжатой зоны:
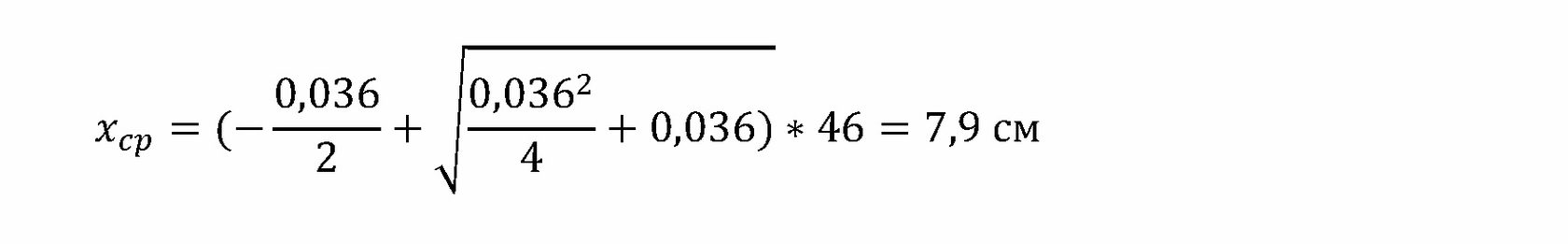
Значение коэффициента φ принимается по таблице 8.8 по величине σ.
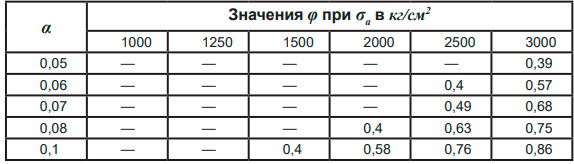
Таблица 8.8 – Значения коэффициента φ
При а = 0,05 – φ = 0,39
3. Теперь рассчитаем Вкр по формуле 8.8:
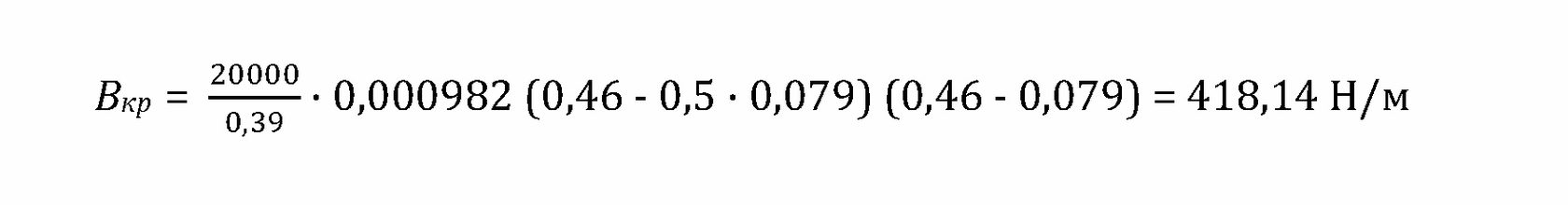
Вкр = 20000/0,39 · 0,000982 (0,46 - 0,5 · 0,079) (0,46 - 0,079) = 418,14 Н/м 4.
Теперь рассчитаем жесткость В по формуле (8.7):

В = 48,14 40000/(40000·2+0,5·0,4·25000)=222,7 Н/м
5. Далее рассчитаем прогиб ригеля f :

где l – пролёт балки, l = 6 м.
Подставляя значения, получаем
f=(5·40000·6)/(384 ·222,7)=0,027 м
Значения прогибов не должно превышать предельных значений:
f≤l/200
0,027 м < 0,03 м – условие выполняется.