Нагрузка на перекрытие q = 320 кг/м2 = 3,2 кН/м2
Материал – влажная ель.
Ширина b = 100 мм (из двух досок толщиной 50 мм) = 0,10 м.
Определить высоту сечения h.
Расчетная схема
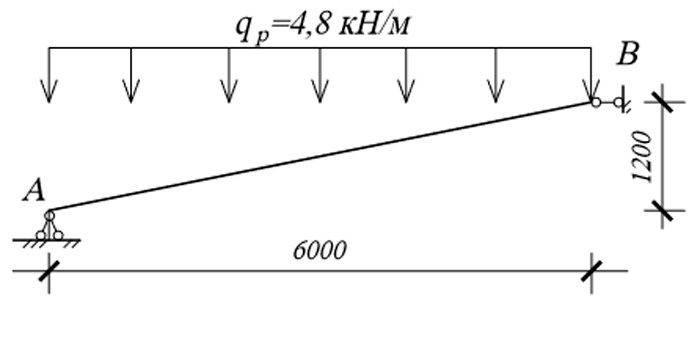
Рисунок 8.20 –Расчетная схема деревянной балки
Расчетная нагрузка:
Qр = 3,2 кН/м2 ·1,5 м (шаг стропил) = 4,8 кН/м.
Подбор сечения балки
Расчет внецентренно сжатых цельных элементов:
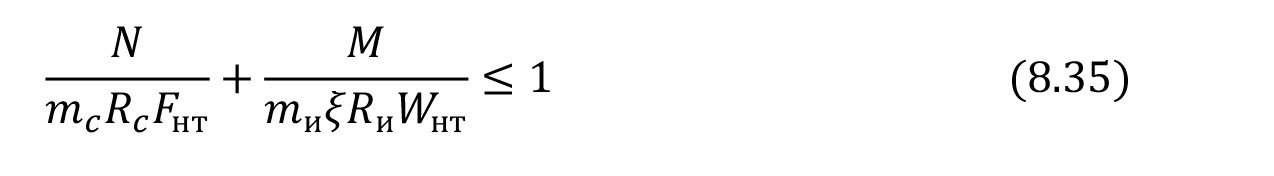
где ξ – коэффициент (от 0 до 1), учитывающий дополнительный момент от расчетной продольной силы N при деформации элемента, определяемый по формуле (8.36):

λ - гибкость элемента, определяется по формуле (8.37);

Используем предельно допустимую гибкость, равную 70.
Fбр – площадь поперечного сечения брутто элемента;
i бр –момент инерции поперечного сечения брутто элемента;
mc =1- коэффициент условий работы элементов на сжатие ;
Rс =130 кг/см2 = 13 Мпа=13000 кН/м2 – расчетное сопротивление древесины сжатию вдоль волокон, принимаемое по таблице 8.31.
Fнт – площадь сечения нетто (ослабления, расположенные на участке длиной 20 см, принимаются совмещенными в одном сечении);

Пусть h = 0,4м, тогда по формуле 8.38:
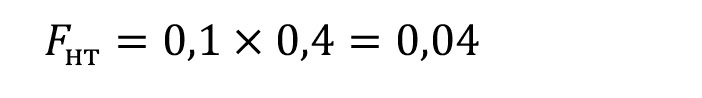
mи = 1,15– коэффициент условий работы элемента на изгиб, принимаемый равным 1, за исключением брусьев с размером сторон 15 см и более, для которых mи = 1,15, и бревен, не имеющих врезок в расчетном сечении, для которых mи = 1,2.
Rи =130 кг/см2 = 13 МПа - расчетное сопротивление древесины изгибу, принимаемое по таблице 8.31;
Wнт – момент сопротивления сечения элемента нетто;
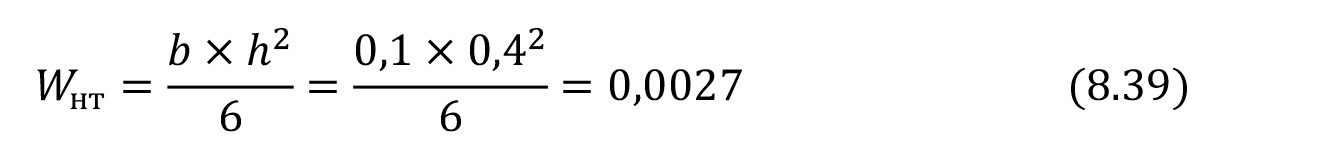
М и N – расчетный изгибающий момент и расчетная продольная сила
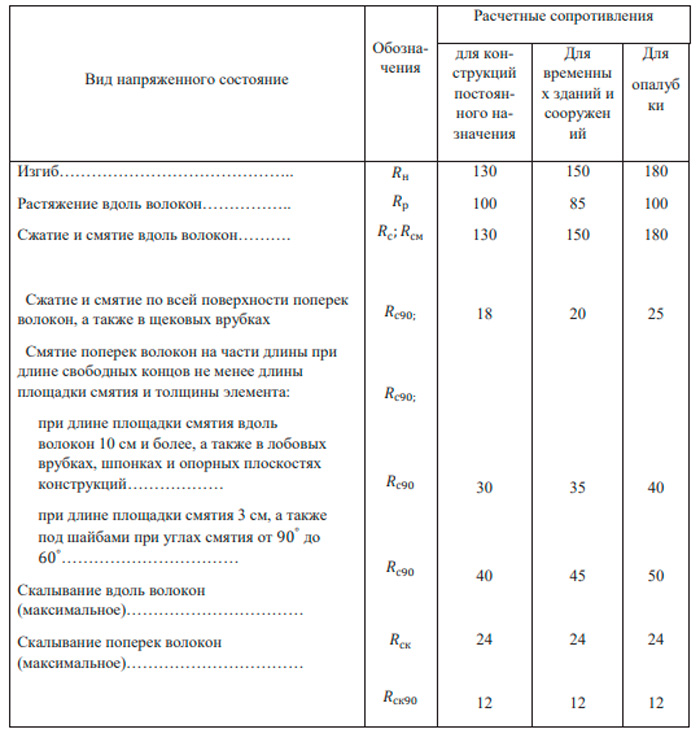
Таблица 8.31 – Основные расчетные сопротивления древесины сосны и ели в кг/см2
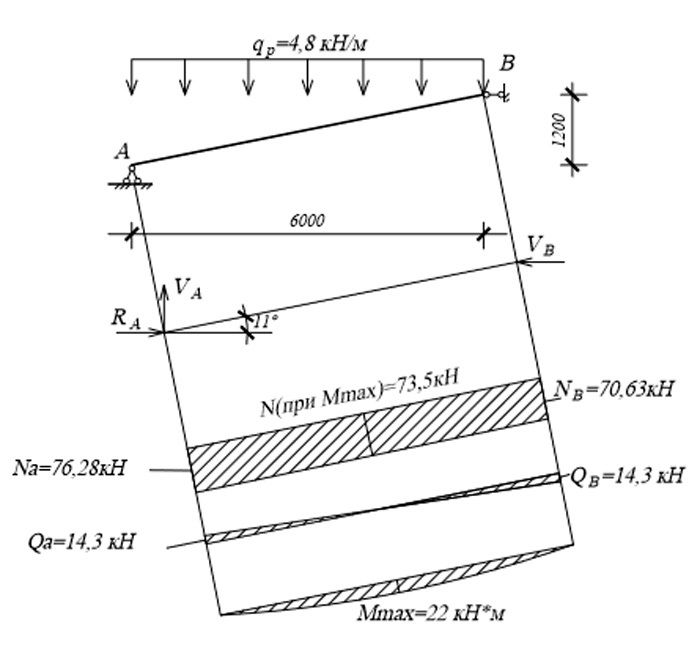
Рисунок 8.21 – Эпюры усилий
q = 320 кг/м2 = 3,2 кН/м2
qр = 3,2 кН/м2 ·1,5 м (шаг стропил) = 4,8 кН/м.
sin11°= 0,9810, сos11°= 0,19389
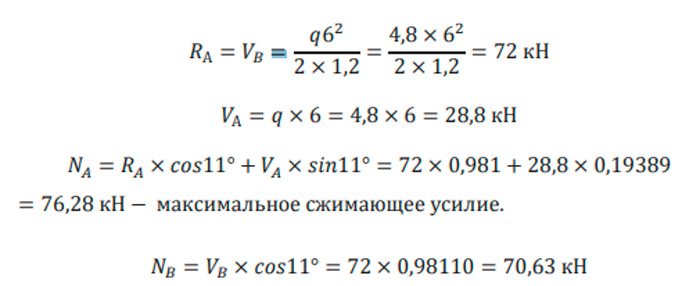
Максимальный изгибающий момент будет возникать в месте, где Q (поперечная сила) равна нулю.
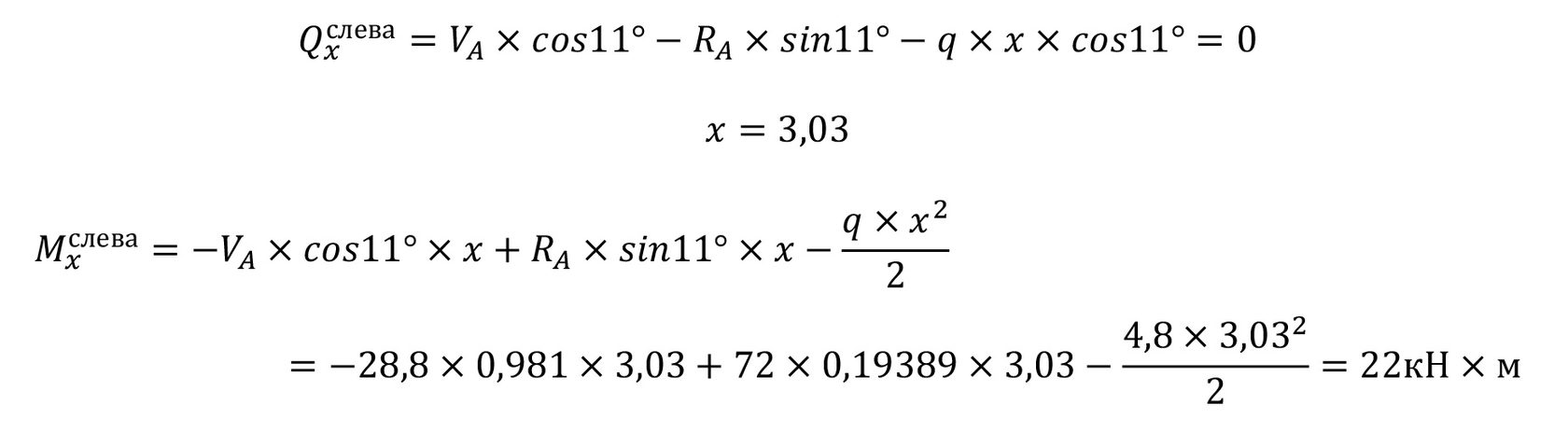
Продольная сила при максимальном моменте равна 73,5 кН (по эпюре). Подставим найденные усилия в формулы (8.35 и 8.36):
